This year’s, qual round of HackToday had around 30 challenges created by 10 problem setters. I made 4 of them – 3 crypto challenges and 1 misc challenge.
To add some innovation and hype up the participants, I created a First Blood Bot called BotToday for the HackToday 2021 Discord server. Even though the bot was only made 4 days before the qual round, it worked perfectly without any major issues during the competition.
This writeup contains the solutions for these challenges:
- crypto🍞 (465 points, 6 solves): Custom Random Number Generator (RNG)
- PKX (500 points, 1 solve): Small subgroup attack on Diffie-Hellman
- bookmove (500 points, 0 solves): Dependent primes in RSA
Notes:
- The solve counts shown below are from the frozen leaderboard
- Hints in the challenge descriptions were released when no team had solved them yet
crypto🍞 (465 points, 6 solves)
Please rate our 🍞. Thank you!
Author: deomkicer#3362
#!/usr/bin/env python3
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from Crypto.Util.number import getRandomNBitInteger
FLAG = open('flag.png', 'rb').read()
class Bread:
def __init__(self, state, switch=True):
assert state.bit_length() <= 64
self.state = state
self.switch = switch
self.mask32 = (1 << 32) - 1
self.mask64 = (1 << 64) - 1
def encrypt(self, message):
key = b''.join([int.to_bytes(self.next(), 4, 'big') for _ in range(4)])
iv = b''.join([int.to_bytes(self.next(), 4, 'big') for _ in range(4)])
cipher = AES.new(key, AES.MODE_CBC, iv)
return iv + cipher.encrypt(pad(message, 16))
def next(self):
self.state = ((self.state << 43) | (self.state >> (64 - 43))) & self.mask64
self.state = self.state ^ int.from_bytes('🍞'.encode(), 'big')
self.switch = not self.switch
return (self.state >> 32) & self.mask32 if self.switch else self.state & self.mask32
def main():
seed = getRandomNBitInteger(64)
bread = Bread(seed)
enc = bread.encrypt(FLAG)
with open('flag.enc', 'wb') as f:
f.write(enc)
f.close()
if __name__ == '__main__':
main()
Solution
The RNG is initialized with a random 64-bit seed. Each time self.next is called, the self.state value changes due to bit rotation and XOR with 🍞. The value returned by self.next alternates between the first 32 bits and last 32 bits of self.state.
def encrypt(self, message):
key = b''.join([int.to_bytes(self.next(), 4, 'big') for _ in range(4)])
iv = b''.join([int.to_bytes(self.next(), 4, 'big') for _ in range(4)])
cipher = AES.new(key, AES.MODE_CBC, iv)
return iv + cipher.encrypt(pad(message, 16))
From the code above, we can see that self.next is called 8 times (4 for the key, 4 for the IV). The self.encrypt function also prepends the IV when returning the encrypted flag. This means we have 4 half-state values (32-bit states 5 through 8) generated by the RNG. The main idea of this challenge is to find the 4 previous half-states (32-bit states 1 through 4) which are used as the AES-CBC key.
Note: I call them half-states because self.next only returns 32 bits from the 64-bit self.state.
First, let’s get the 4 half-state values from the IV.
enc = open('flag.enc', 'rb').read()
iv, enc = enc[:16], enc[16:]
print(f'iv: {iv.hex()}')
states = [int.from_bytes(iv[x:x+4], 'big') for x in range(0, len(iv), 4)]
for state in states:
print(bin(state)[2:].zfill(32))
iv: a5717f138bf89aa2344a9eb054f58146
10100101011100010111111100010011
10001011111110001001101010100010
00110100010010101001111010110000
01010100111101011000000101000110
On the first self.next call, self.switch is set to False, so we can see that half-states 1, 3, 5, and 7 are the last 32 bits of the full state. Meanwhile, half-states 2, 4, 6, and 8 are the first 32 bits of the full state. Let’s try to manually arrange the bits of full states 1 through 8. Unknown bits will be marked with dashes.
state 1: ----------------------------------------------------------------
state 2: ----------------------------------------------------------------
state 3: ----------------------------------------------------------------
state 4: ----------------------------------------------------------------
state 5: --------------------------------10100101011100010111111100010011
state 6: 10001011111110001001101010100010--------------------------------
state 7: --------------------------------00110100010010101001111010110000
state 8: 01010100111101011000000101000110--------------------------------
We can see that the first 21 bits of state 6 match the last 21 bits of state 5. This happens because of the bit rotation done when calling self.next. So, bits 21-32 in state 6 must be exactly the same as the first 11 bits in state 5. The same applies to states 7 and 8.
state 1: ----------------------------------------------------------------
state 2: ----------------------------------------------------------------
state 3: ----------------------------------------------------------------
state 4: ----------------------------------------------------------------
state 5: 01010100010---------------------10100101011100010111111100010011
state 6: 10001011111110001001101010100010--------------------------------
state 7: 00101000110---------------------00110100010010101001111010110000
state 8: 01010100111101011000000101000110--------------------------------
At this point, we’ve recovered 11 more bits in state 5, leaving only 21 unknown bits. Since we only have 21 bits left, we can brute force the full state 5. We do this by using state 5 as the initial RNG state in each iteration, generate 3 half-states, then compare them with the known half-states (half-states 6, 7, and 8).
state_5_hole = states[0] | ((states[1] & ((1 << 11) - 1)) << (64 - 11))
print(f'bin_state_5_hole: {bin(state_5_hole)[2:].zfill(64)}')
for i in range(2**21):
state_5_test = state_5_hole | (i << 32)
a = Bread(state_5_test, False)
b = [a.next() for _ in range(3)]
if b == states[1:]:
state_5 = state_5_test
break
print(f'state_5: {state_5}')
print(f'bin_state_5_full: {bin(state_5)[2:].zfill(64)}')
bin_state_5_hole: 0101010001000000000000000000000010100101011100010111111100010011
state_5: 6076107218727567123
bin_state_5_full: 0101010001010010101010110101001010100101011100010111111100010011
state 1: ----------------------------------------------------------------
state 2: ----------------------------------------------------------------
state 3: ----------------------------------------------------------------
state 4: ----------------------------------------------------------------
state 5: 0101010001010010101010110101001010100101011100010111111100010011
state 6: 10001011111110001001101010100010--------------------------------
state 7: 00101000110---------------------00110100010010101001111010110000
state 8: 01010100111101011000000101000110--------------------------------
After successfully finding the complete full state 5, we need to reverse the bit rotation and XOR process, which is pretty straightforward to implement. We do this 5 times until we get the original initial state used by the program to encrypt the flag.
seed = state_5
for _ in range(5):
seed = seed ^ int.from_bytes('🍞'.encode(), 'big')
seed = ((seed << 21) | (seed >> (64 - 21))) % (1 << 64)
print(f'seed: {seed}')
Implementation
#!/usr/bin/env python3
from Crypto.Cipher import AES
from Crypto.Util.Padding import unpad
from chall import Bread
enc = open('flag.enc', 'rb').read()
iv, enc = enc[:16], enc[16:]
print(f'iv: {iv.hex()}')
states = [int.from_bytes(iv[x:x+4], 'big') for x in range(0, len(iv), 4)]
print(states)
state_5_hole = states[0] | ((states[1] & ((1 << 11) - 1)) << (64 - 11))
print(f'bin_state_5_hole: {bin(state_5_hole)[2:].zfill(64)}')
for i in range(2**21):
state_5_test = state_5_hole | (i << 32)
a = Bread(state_5_test, False)
b = [a.next() for _ in range(3)]
if b == states[1:]:
state_5 = state_5_test
break
print(f'state_5: {state_5}')
print(f'bin_state_5_full: {bin(state_5)[2:].zfill(64)}')
seed = state_5
for _ in range(5):
seed = seed ^ int.from_bytes('🍞'.encode(), 'big')
seed = ((seed << 21) | (seed >> (64 - 21))) % (1 << 64)
print(f'seed: {seed}')
a = Bread(seed)
calc_key = b''.join([int.to_bytes(a.next(), 4, 'big') for _ in range(4)])
calc_iv = b''.join([int.to_bytes(a.next(), 4, 'big') for _ in range(4)])
assert calc_iv == iv
print(f'key: {calc_key.hex()}')
cipher = AES.new(calc_key, AES.MODE_CBC, calc_iv)
res = unpad(cipher.decrypt(enc), 16)
with open('result.png', 'wb') as f:
f.write(res)
f.close()
$ python3 solve.py
iv: a5717f138bf89aa2344a9eb054f58146
[2775678739, 2348325538, 877305520, 1425375558]
bin_state_5_hole: 0101010001000000000000000000000010100101011100010111111100010011
state_5: 6076107218727567123
bin_state_5_full: 0101010001010010101010110101001010100101011100010111111100010011
seed: 11800126609623179686
key: e35a8027d4013e58f96d49576a4abdde
Flag
hacktoday{we_baked_bread_you_cant_refuse}
PKX (500 points, 1 solve)
Sebuah percakapan antara sepasang anak muda di tanah sunda. Karena maraknya penyadapan komunikasi terjadi, mereka pun mengenkripsi percakapan mereka menggunakan metode Punten Key eXchange (PKX).
nc 103.41.207.206 11005
Author: deomkicer#3362
#!/usr/bin/env python3
from Crypto.Cipher import AES
from Crypto.Hash import SHA1
from Crypto.Util.number import *
from Crypto.Util.Padding import pad
import math
import sys
class Unbuffered(object):
def __init__(self, stream):
self.stream = stream
def write(self, data):
self.stream.write(data)
self.stream.flush()
def writelines(self, datas):
self.stream.writelines(datas)
self.stream.flush()
def __getattr__(self, attr):
return getattr(self.stream, attr)
sys.stdout = Unbuffered(sys.stdout)
FLAG = open('flag.txt', 'rb').read()
class PKX:
def __init__(self, p):
self.g = 0x24e6e064ca1d3dac
self.p = p
assert self.g < self.p
self.private = getRandomRange(2, self.p - 2)
self.secret = None
def getPublicKey(self):
return pow(self.g, self.private, self.p)
def getSharedSecret(self, x):
assert x > 1 and x < self.p - 1
self.secret = pow(x, self.private, self.p)
def getFingerprint(self):
return SHA1.new(long_to_bytes(self.secret)).hexdigest()
def checkFingerprint(self, fingerprint):
return fingerprint == self.getFingerprint()
def encrypt(self, msg):
iv = AES.get_random_bytes(AES.block_size)
key = SHA1.new(long_to_bytes(self.secret)).digest()[:16]
cipher = AES.new(key, AES.MODE_CBC, iv)
return iv.hex() + cipher.encrypt(pad(msg, 16)).hex()
def check(p, k):
for _ in range(k):
if not isPrime(p):
return False
d = int(math.log10(p))
p = p - p // pow(10, d) * pow(10, d)
return True
def user_input(s):
inp = input(s).strip()
assert len(inp) <= 64, 'You may send up to 64 digits for PKX prime.'
return inp
def main():
print('+' + '-'*60)
print('| Welcome to Punten Key eXchange (PKX)!')
print('| We ensure only Alice and Bob can read or listen to what is sent, and nobody in between, not even us.')
print('+' + '-'*60)
p = int(user_input('| Please enter a PKX prime: '))
print('+' + '-'*60)
if not check(p, 20) or p < 0:
print('| That\'s not a PKX prime.')
print('+' + '-'*60)
return
Alice = PKX(p)
Bob = PKX(p)
A = Alice.getPublicKey()
B = Bob.getPublicKey()
print('| Alice\'s public key: ' + chr(42)*10 + hex(A)[2:].zfill(len(hex(p)[2:]))[10:])
print('| Bob\'s public key: ' + chr(42)*10 + hex(B)[2:].zfill(len(hex(p)[2:]))[10:])
print('+' + '-'*60)
Alice.getSharedSecret(B)
Bob.getSharedSecret(A)
if Bob.checkFingerprint(Alice.getFingerprint()):
print('| Bob: ' + Bob.encrypt(b'Hey Alice, can you give me the flag?'))
print('| Alice: ' + Alice.encrypt(b'Sure, Bob. Here is the flag: ' + FLAG))
print('| Bob: ' + Bob.encrypt(b'Hatur nuhun teh Alis.'))
print('| Alice: ' + Alice.encrypt(b'Sami-sami kang Bobi.'))
else:
print('| Fingerprint mismatch.')
print('+' + '-'*60)
if __name__ == '__main__':
main()
Solution
We’re given the server.py code and a service at 103.41.207.206 11005. In the provided source code, Alice and Bob’s communication is encrypted using AES-CBC, and Diffie-Hellman key exchange is involved in their key exchange process.
In this challenge, the Diffie-Hellman parameter $ p $ is determined by user input, while the parameter $ g $ is constant in the source code with an ‘unusual’ value of $ \mathrm{0x24e6e064ca1d3dac} $. Before diving deeper into the relationship between parameters $ g $ and $ p $ in Diffie-Hellman, let’s try to find a value of $ p $ that passes the check.
def check(p, k):
for _ in range(k):
if not isPrime(p):
return False
d = int(math.log10(p))
p = p - p // pow(10, d) * pow(10, d)
return True
if not check(p, 20) or p < 0:
print('| That\'s not a PKX prime.')
print('+' + '-'*60)
return
Looking at the check function, it verifies if $ p $ is a prime number in each iteration. If it is prime, the first digit of $ p $ is removed, then it moves to the next iteration. If it’s not prime, the check function immediately returns False. This shows that the check function is looking for a 20-digit left-truncatable prime. Generating truncatable primes is pretty straightforward to implement in Python or Sage. Here’s the code:
pkx = []
res = ['']
while True:
tmp = []
for i in res:
for j in '123456789':
if is_prime(int(j+i)):
tmp.append(j+i)
res = tmp
if not res: break
if len(res[0]) >= 20: pkx += res
pkx = list(map(int, pkx))
print(pkx, len(pkx))
[36484957213536676883, 67986315421273233617, 86312646216567629137, 18918997653319693967, 15396334245663786197, 66276812967623946997, 367986315421273233617, 686312646216567629137, 918918997653319693967, 315396334245663786197, 666276812967623946997, 6686312646216567629137, 7686312646216567629137, 5918918997653319693967, 9918918997653319693967, 96686312646216567629137, 57686312646216567629137, 95918918997653319693967, 357686312646216567629137] 19
There are 19 (or maybe more?) possible numbers that return True in the check function. The code above generates truncatable primes with 20 digits or more, because 21-digit truncatable primes will still return True when checked with the check function (as per Hint 1), and so on.
In [3]: def check(p, k):
...: for _ in range(k):
...: if not isPrime(p):
...: return False
...: d = int(math.log10(p))
...: p = p - p // pow(10, d) * pow(10, d)
...: return True
...:
In [4]: check(36484957213536676883, 20)
Out[4]: True
In [5]: check(357686312646216567629137, 20)
Out[5]: True
According to Hint 2, which of these 19 numbers would help us find the shared secret? Since we don’t get Alice and Bob’s complete public keys, we can’t use this to get their private keys by calculating the discrete log. With the public keys unknown and the $ p $ parameter under our control, we can implement a small subgroup attack between parameters $ g $ and $ p $.
We can use Sage’s discrete-log module to quickly calculate the subgroup size formed between $ g $ and $ p $ (though I’m sure this isn’t the optimal way). Here’s the code:
sage: ps = [36484957213536676883, 67986315421273233617, 86312646216567629137, 18918997653319693967, 153963342456637861
....: 97, 66276812967623946997, 367986315421273233617, 686312646216567629137, 918918997653319693967, 31539633424566378
....: 6197, 666276812967623946997, 6686312646216567629137, 7686312646216567629137, 5918918997653319693967, 99189189976
....: 53319693967, 96686312646216567629137, 57686312646216567629137, 95918918997653319693967, 357686312646216567629137
....: ]
sage: g = 0x24e6e064ca1d3dac
sage: for p in ps:
....: P = GF(p)
....: subgroup_size = (P(g)^-1).log(P(g))
....: print(p, subgroup_size)
....:
36484957213536676883 36484957213536676881
67986315421273233617 67986315421273233615
86312646216567629137 28770882072189209711
18918997653319693967 18918997653319693965
15396334245663786197 7698167122831893097
66276812967623946997 33138406483811973497
367986315421273233617 22999144713829577100
686312646216567629137 42894540388535476820
918918997653319693967 918918997653319693965
315396334245663786197 315396334245663786195
666276812967623946997 666276812967623946995
6686312646216567629137 1671578161554141907283
7686312646216567629137 3843156323108283814567
5918918997653319693967 2959459498826659846982
9918918997653319693967 4959459498826659846982
96686312646216567629137 52500
57686312646216567629137 3204795147012031534951
95918918997653319693967 15986486499608886615660
357686312646216567629137 44710789080777070953641
We can see that the pair of values $ g $ with the prime number $ 96686312646216567629137 $ produces a subgroup that is much smaller compared to other prime numbers, so we’ll use this prime number as the value of $ p $.
Since the subgroup size is only 52500 (more precisely 52501 because the number 1 in the group is still counted) and this range is very brute-forcible, we can directly brute-force the shared secret between Alice and Bob using the parameters $ g = \mathrm{0x24e6e064ca1d3dac} $ and $ p = 96686312646216567629137 $. Here’s the code.
Implementation
#!/usr/bin/sage
from Crypto.Cipher import AES
from Crypto.Hash import SHA1
from Crypto.Util.number import long_to_bytes
from pwn import *
import time
start = time.time()
pkx = []
res = ['']
while True:
tmp = []
for i in res:
for j in '123456789':
if is_prime(int(j+i)):
tmp.append(j+i)
res = tmp
if not res: break
if len(res[0]) >= 20: pkx += res
pkx = list(map(int, pkx))
print(pkx, len(pkx))
g = 0x24e6e064ca1d3dac
min_s = 2^64
for p in pkx:
P = GF(p)
s = (P(g)^-1).log(P(g)) # bukan cara yang paling optimal
if s < min_s:
min_p = p
min_s = s
assert min_s < 2^16
p = min_p
print(f'{p = }')
s = min_s
print(f'{s = }')
# r = process('./server.py')
# r = remote('localhost', 11005)
r = remote('103.41.207.206', 11005)
r.sendlineafter(b'Please enter a PKX prime: ', str(p).encode())
r.recvuntil(b'Bob: ')
r.recvuntil(b'Alice: ')
enc = bytes.fromhex(r.recvline(0).decode())
iv, ct = enc[:16], enc[16:]
r.close()
for x in range(s):
y = pow(g, x, p)
key = SHA1.new(long_to_bytes(y)).digest()[:16]
cipher = AES.new(key, AES.MODE_CBC, iv)
pt = cipher.decrypt(ct)
if b'flag' in pt:
flag = pt[pt.index(b'hacktoday{'):pt.index(b'}')+1]
print(f'flag = {flag.decode()}')
break
end = time.time()
print(f'time = {end-start} seconds')
$ sage solve.sage
[36484957213536676883, 67986315421273233617, 86312646216567629137, 18918997653319693967, 15396334245663786197, 66276812967623946997, 367986315421273233617, 686312646216567629137, 918918997653319693967, 315396334245663786197, 666276812967623946997, 6686312646216567629137, 7686312646216567629137, 5918918997653319693967, 9918918997653319693967, 96686312646216567629137, 57686312646216567629137, 95918918997653319693967, 357686312646216567629137] 19
p = 96686312646216567629137
s = 52500
[x] Opening connection to 103.41.207.206 on port 11005
[x] Opening connection to 103.41.207.206 on port 11005: Trying 103.41.207.206
[+] Opening connection to 103.41.207.206 on port 11005: Done
[*] Closed connection to 103.41.207.206 port 11005
flag = hacktoday{all_your_conversation_are_belong_to_us}
time = 8.173951625823975 seconds
Flag
hacktoday{all_your_conversation_are_belong_to_us}
bookmove (500 points, 0 solves)
Definitely the conventional moves.
Author: deomkicer#3362
#!/usr/bin/env python3
from Crypto.Util.number import bytes_to_long, isPrime, getPrime
from libnum import grey_code
FLAG = open('flag.txt', 'rb').read()
def bookmove(nbit):
while True:
p = getPrime(nbit // 3)
if p % 8 == 1:
q = grey_code(p)
r = grey_code(q)
if isPrime(q) and isPrime(r):
return p * q * r
m = bytes_to_long(FLAG)
e = 65537
n = bookmove(1536)
c = pow(m, e, n)
print(f'{e = }')
print(f'{n = }')
print(f'{c = }')
e = 65537
n = 1337019719866013134311502867665167638966695743292894716327343862274121579466869813594221725755438050073939953340753287213906421339262574483387468763195012360339971640277270196638499163755345814097026097936673955162469055482078476651059809508489652783985615153221495580490730931660705593609939955424611697354621729662929558565499366483826261600300167171392762299060817265964348661751639430527513341508915893730214795480676247679224372484041466733871469573310022179
c = 308013715706893096316943745042644246712394567314503581147341487424999022679742698959777178713510471886312316680638653501601294983972427880095230642174257809555165327207166272407873917975855381008065455831026725087298871408371006858974416002264387201821745372781658202601775263720561069642128144635638590920742252564219016677475961650093872263358830241576866286716368280154739111992549611084155614682637575573462749366166200569569916981088019443740751232359060185
Solution
We’re given the code chall.py and output.txt. The program encrypts the flag using RSA where the modulus $ n $ is the product of three prime numbers $ p, q, $ and $ r $.
First, let’s understand the grey_code function from one of the repositories by the crypto god, hellman. The grey_code function is quite simple – it XORs $ n $ with $ n $ shifted right by 1 bit.
def grey_code(n):
return n ^ (n >> 1)
Simply, \(\mathrm{bit}_i\) is obtained from XORing \(\mathrm{bit}_{i+1}\) and \(\mathrm{bit}_{i}\) (bit order from right to left). Here’s an illustration when $ p = 17 $ ($ p $ must satisfy $ p = 1\pmod{8} $ for $ q $ and $ r $ to be odd numbers).
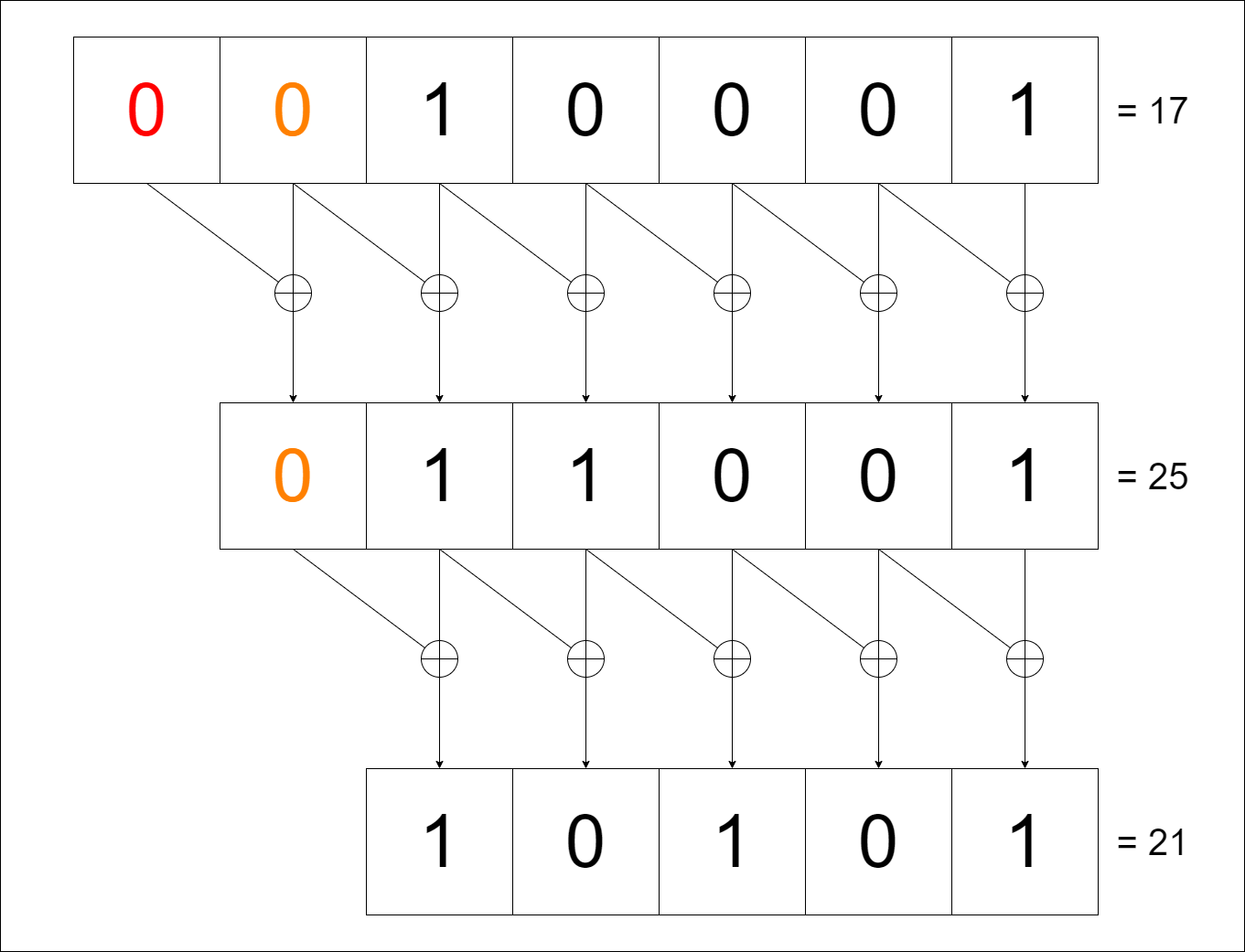
In [1]: from libnum import *
In [2]: p = 17
In [3]: q = grey_code(p); q
Out[3]: 25
In [4]: r = grey_code(q); r
Out[4]: 21
Remember! If $ A \times B = C $, then $ (A \pmod{n} \times B \pmod{n}) \pmod{n} = C \pmod{n} $. Here’s an example.

Notes:
- This rule applies not only in base 10 (decimal) but also in other bases, including base 2 (binary).
- The mask function represents $ \pmod{n} $
mask = lambda a, x: a & ((1 << x) - 1)
According to the hint, we can brute-force the value of $ p $ bit by bit (or several bits at a time), then generate values for $ q $ and $ r $ based on the value of $ p $ in each iteration, multiply these three numbers with a certain bit mask, and compare with $ n $. However, this becomes a bit tricky because the additional bits of $ p $ are not necessarily 0. This is because $ p $ has additional bits that cannot be determined as either 0 or 1. Since the MSB of $ r $ depends on the additional bit of $ q $, and the additional bit of $ q $ depends on 2 additional bits of $ p $, we also need to brute-force 2 additional bits of $ p $ simultaneously to find the values of $ p, q, $ and $ r $.
Implementation
#!/usr/bin/python
from libnum import *
exec(open('output.txt').read())
mask = lambda a, x: a & ((1 << x) - 1)
grey = lambda p: p ^ (p >> 1)
def cari(curr_p, x):
for i in range(1024): # 2^8, plus 2 additional bits
test_p = int(bin(i)[2:].zfill(10) + curr_p, 2)
test_q = grey(test_p)
test_r = grey(test_q)
if mask(test_p * test_q * test_r, x) == mask(n, x):
res = []
res.append(bin(mask(test_p, x))[2:].zfill(x))
res.append(bin(mask(test_q, x))[2:].zfill(x))
res.append(bin(mask(test_r, x))[2:].zfill(x))
return res
x = 8
curr_p = ''
curr_q = ''
curr_r = ''
while True:
res = cari(curr_p, x)
curr_p = res[0]
curr_q = res[1]
curr_r = res[2]
print '>', x
print 'curr_p =', int(curr_p, 2)
print 'curr_q =', int(curr_q, 2)
print 'curr_r =', int(curr_r, 2)
print
x += 8
if int(curr_p, 2) * int(curr_q, 2) * int(curr_r, 2) == n:
break
print '> found'
p = int(curr_p, 2)
q = int(curr_q, 2)
r = int(curr_r, 2)
d = invmod(e, (p-1) * (q-1) * (r-1))
print n2s(pow(c, d, n))
$ python solve.py
> 8
curr_p = 89
curr_q = 245
curr_r = 143
> 16
curr_p = 25433
curr_q = 21237
curr_r = 31631
> 24
curr_p = 549721
curr_q = 9196277
curr_r = 13269903
> 32
curr_p = 1393058649
curr_q = 4203500277
curr_r = 130710415
...
> 488
curr_p = 554054447595710955666362614793081391948235276695164364263933630596038736909443490751734691988505547874267136360512740792657926409305152129285514073
curr_q = 729792514060899554983983679451720106970684641220561153869779206263317824732325887619762106197450825811608408555272166998460027403137846098139042549
curr_r = 490574122930329477293669224898904798318425476956172102596126144965021805701429369739763706555878213410841983672525957931725488750641845007934978959
> 496
curr_p = 163584250739298089247338896343511398543363024679230617746732546690071452425032883235914600618376310249725068787244852214884533008284456563964983665497
curr_q = 34294832927058448026798917094187844226379611871154330967907434836155314760522445835153293326336116499722067571972636176370316661906845489711371014901
curr_r = 50838134742426652185016069347003090977431816321856826823652609589803017209386609291040060536763876724276530728798571971989510440506203310427782937487
> 504
curr_p = 40876379936447562597536385750636775854237848472339848936945168937385735545208172659596586373921809264813878202623773235392024161297734032664738545558361
curr_q = 33586548563862512615661993309577079154446960583812568423171643957821526727908436633388671739666853727296310579879463364020847196257232124286328778806005
curr_r = 50379218731145607903637807658071340056308303274233977965129257394067860136931257890621317730047540292919159299190034663738704829833494121505353894624143
> 512
curr_p = 11563211319730866945043964118583785791656817850543927907918130784635776698889662605848707311361104442435935006331635223187836767202814317580381155660161881
curr_q = 9356202999852074558413226249874579464667443507714461088871585460295610578888421568940941894683841893293021586975170545598271593838938831540165975353348853
curr_r = 12358327904420639039153231067729844152390882396396157586422304801435530934618507584251716864875447171180253091618815901658395589442362572002020617630677903
> found
hacktoday{your_book_move_reached_the_512_bit_depth}
Flag
hacktoday{your_book_move_reached_the_512_bit_depth}
