CryptoCTF is an annual CTF event organized by ASIS since 2019, and it only focuses on cryptography problems. This year, CryptoCTF was held on July 30-31, 2021, in a 24-hour Jeopardy format.
This writeup covers solutions for these challenges:
- Mic Check (warm-up)
- Farm (easy): Finite Field
- KeyBase (easy): Block chaining and IV recovery in AES-CBC
- Symbols (easy): LaTeX
- Hamul (easy-medium): Dependent primes in RSA
- Rima (easy-medium): Bit manipulation
- Tuti (medium): Diophantine equations
- Ferman (medium): Brahmagupta-Fibonacci identity
- Salt and Pepper (medium): Hash length extension attack
- Wolf (medium-hard): Improper nonce implementation in AES-GCM
Mic Check
The flag was on the CryptoCTF rules page.
CCTF{W3lc0me_t0_The_0ne_&_0nly_Crypt0_CTF_Mad3ـw1th_L0ve_f0r_Crypt0!}
Farm
We get farm.sage and enc.txt files.
#!/usr/bin/env sage
from sage.all import *
import string, base64, math
from flag import flag
ALPHABET = string.printable[:62] + '\\='
F = list(GF(64))
def keygen(l):
key = [F[randint(1, 63)] for _ in range(l)]
key = math.prod(key) # Optimization the key length :D
return key
def maptofarm(c):
assert c in ALPHABET
return F[ALPHABET.index(c)]
def encrypt(msg, key):
m64 = base64.b64encode(msg)
enc, pkey = '', key**5 + key**3 + key**2 + 1
for m in m64:
enc += ALPHABET[F.index(pkey * maptofarm(chr(m)))]
return enc
# KEEP IT SECRET
key = keygen(14) # I think 64**14 > 2**64 is not brute-forcible :P
enc = encrypt(flag, key)
print(f'enc = {enc}')
enc = 805c9GMYuD5RefTmabUNfS9N9YrkwbAbdZE0df91uCEytcoy9FDSbZ8Ay8jj
Solution
The keygen function makes a key by multiplying 14 random numbers between 1 and 63, so the key is around 84 bits. The encryption is pretty unique, each character’s index in the plaintext gets multiplied by the key, and the result is used to pick a character from ALPHABET for the ciphertext. Since the multiplication is done over modulo $ 2^{26} $, it’s actually possible to brute-force it.
Implementation
#!/usr/bin/env sage
import string, base64
ALPHABET = string.printable[:62] + '\\='
target = '805c9GMYuD5RefTmabUNfS9N9YrkwbAbdZE0df91uCEytcoy9FDSbZ8Ay8jj'
F = list(GF(64))
def maptofarm(c):
assert c in ALPHABET
return F[ALPHABET.index(c)]
def encrypt(msg, key):
m64 = msg
enc, pkey = '', key**5 + key**3 + key**2 + 1
for m in m64:
enc += ALPHABET[F.index(pkey * maptofarm(chr(m)))]
return enc
flag = base64.b64encode(b'CCT') # format flag
for key in F:
enc = encrypt(flag, key)
if enc == target[:len(enc)]:
break
print(f'{key = }')
found = True
while found:
found = False
for c1 in ALPHABET:
tmp = c1
test = flag + tmp.encode()
enc = encrypt(test, key)
if enc == target[:len(enc)]:
flag += tmp.encode()
found = True
break
flag = base64.b64decode(flag).decode()
print(f'{flag = }')
$ sage solve.sage
key = z6^5 + 1
flag = 'CCTF{EnCrYp7I0n_4nD_5u8STitUtIn9_iN_Fi3Ld!}'
KeyBase
We get a keybase.py file and a service at 01.cr.yp.toc.tf 17010.
#!/usr/bin/env python3
from Crypto.Util import number
from Crypto.Cipher import AES
import os, sys, random
from flag import flag
def keygen():
iv, key = [os.urandom(16) for _ in '01']
return iv, key
def encrypt(msg, iv, key):
aes = AES.new(key, AES.MODE_CBC, iv)
return aes.encrypt(msg)
def decrypt(enc, iv, key):
aes = AES.new(key, AES.MODE_CBC, iv)
return aes.decrypt(enc)
def die(*args):
pr(*args)
quit()
def pr(*args):
s = " ".join(map(str, args))
sys.stdout.write(s + "\n")
sys.stdout.flush()
def sc():
return sys.stdin.readline().strip()
def main():
border = "+"
pr(border*72)
pr(border, " hi all, welcome to the simple KEYBASE cryptography task, try to ", border)
pr(border, " decrypt the encrypted message and get the flag as a nice prize! ", border)
pr(border*72)
iv, key = keygen()
flag_enc = encrypt(flag, iv, key).hex()
while True:
pr("| Options: \n|\t[G]et the encrypted flag \n|\t[T]est the encryption \n|\t[Q]uit")
ans = sc().lower()
if ans == 'g':
pr("| encrypt(flag) =", flag_enc)
elif ans == 't':
pr("| Please send your 32 bytes message to encrypt: ")
msg_inp = sc()
if len(msg_inp) == 32:
enc = encrypt(msg_inp, iv, key).hex()
r = random.randint(0, 4)
s = 4 - r
mask_key = key[:-2].hex() + '*' * 4
mask_enc = enc[:r] + '*' * 28 + enc[32-s:]
pr("| enc =", mask_enc)
pr("| key =", mask_key)
else:
die("| SEND 32 BYTES MESSAGE :X")
elif ans == 'q':
die("Quitting ...")
else:
die("Bye ...")
if __name__ == '__main__':
main()
Solution
The program gives us 3 options:
- Get the encrypted flag
- Test the encryption
- Quit
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
+ hi all, welcome to the simple KEYBASE cryptography task, try to +
+ decrypt the encrypted message and get the flag as a nice prize! +
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
| Options:
| [G]et the encrypted flag
| [T]est the encryption
| [Q]uit
g
| encrypt(flag) = 438e77d6479cfa357e3fc58fde48028f2dd0bbc5dc2f126db0cb1daf6cd9dd91
| Options:
| [G]et the encrypted flag
| [T]est the encryption
| [Q]uit
t
| Please send your 32 bytes message to encrypt:
00000000000000000000000000000000
| enc = 5f38****************************a71c747cd176a8f66ba5ab69a4cfbadf
| key = 267a269a56464842b12133ae5ca4****
| Options:
| [G]et the encrypted flag
| [T]est the encryption
| [Q]uit
ENCRYPTED_FLAG = '438e77d6479cfa357e3fc58fde48028f2dd0bbc5dc2f126db0cb1daf6cd9dd91'.decode('hex')
ENCRYPTED_ZERO = ['5f38'.decode('hex'), 'a71c747cd176a8f66ba5ab69a4cfbadf'.decode('hex')]
KNOWN_14_KEY = '267a269a56464842b12133ae5ca4'.decode('hex')
On the option 2, we can input any plaintext we want, but it’s limited to 2 blocks (32 bytes). The program will show us:
- The ciphertext, but about 14 bytes from the first block are missing
- The key, but the last 2 bytes are missing
Even though 2 bytes of the key are missing, we can brute-force them by comparing the plaintext-ciphertext pairs we input. The idea is to treat the 2 ciphertext blocks we get as the IV and one ciphertext block. This works because the IV in CBC mode decryption is only used for the XOR with the intermediate state before we get the plaintext.
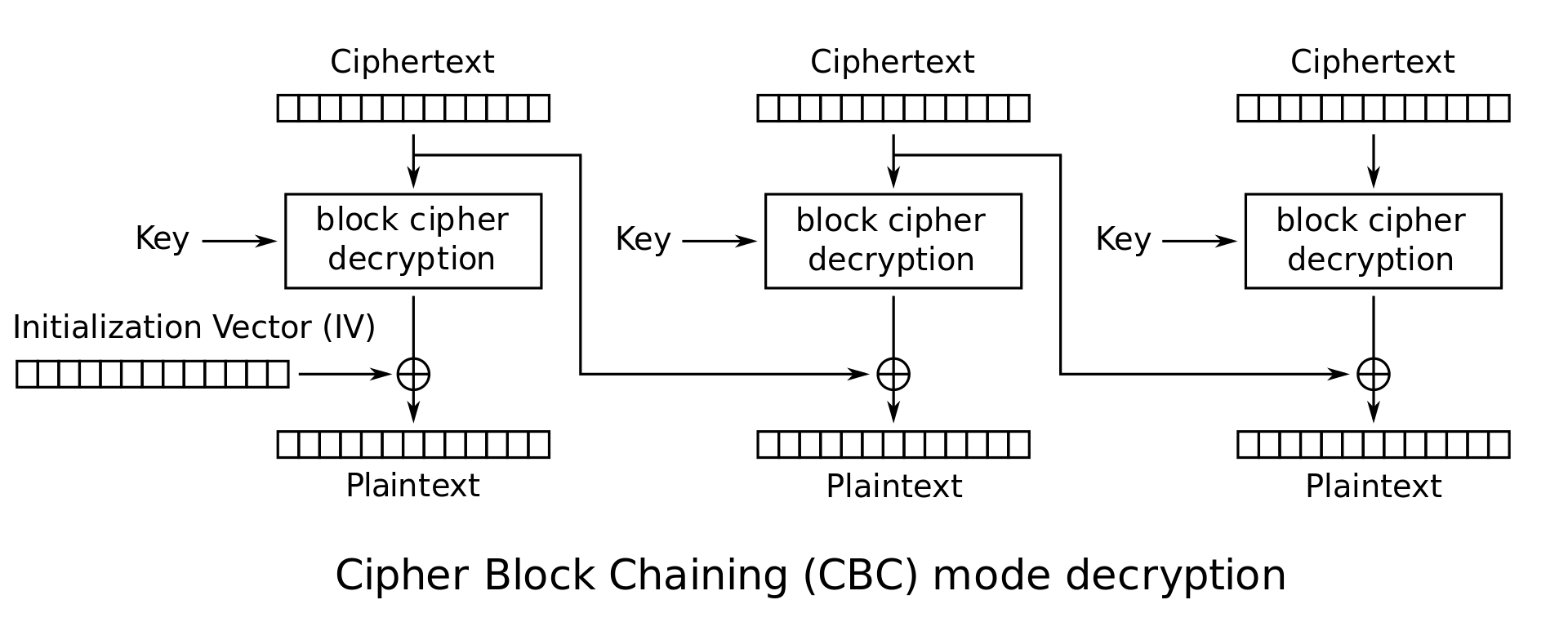
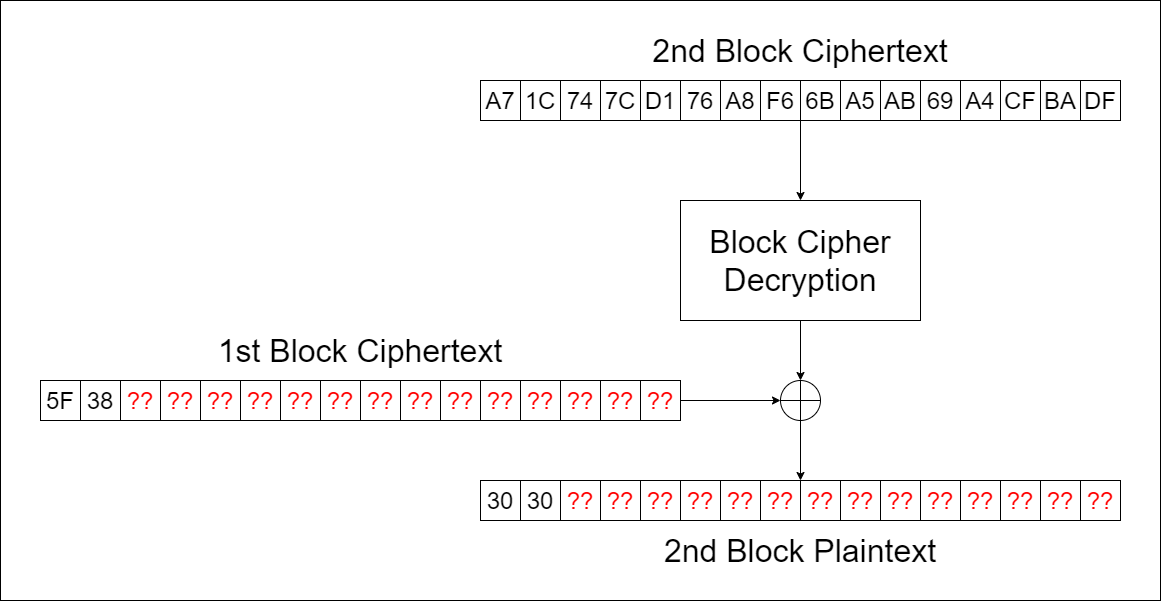
Remember! $ \mathrm{chr}(\mathrm{0x30}) = $ "0".
keys = []
for i in range(256):
for j in range(256):
tmp_key = KNOWN_14_KEY + chr(i) + chr(j)
aes = AES.new(tmp_key, AES.MODE_CBC, tmp_iv)
dec = aes.decrypt(enc)
if dec[:2] == '0'*2:
keys.append(tmp_key)
for key in keys:
aes = AES.new(key, AES.MODE_CBC, ENCRYPTED_FLAG[:16])
res = aes.decrypt(ENCRYPTED_FLAG[16:])
if all(x in string.printable for x in res):
print('key: {}'.format(key.encode('hex')))
break
$ python solve.py
key: 267a269a56464842b12133ae5ca44d52
Once we have the key, the next step is to find the IV. We know the plaintext we input was "0"*32, so "0" can be used to fill in the missing bytes in the first ciphertext block. This works because XOR is reversible.
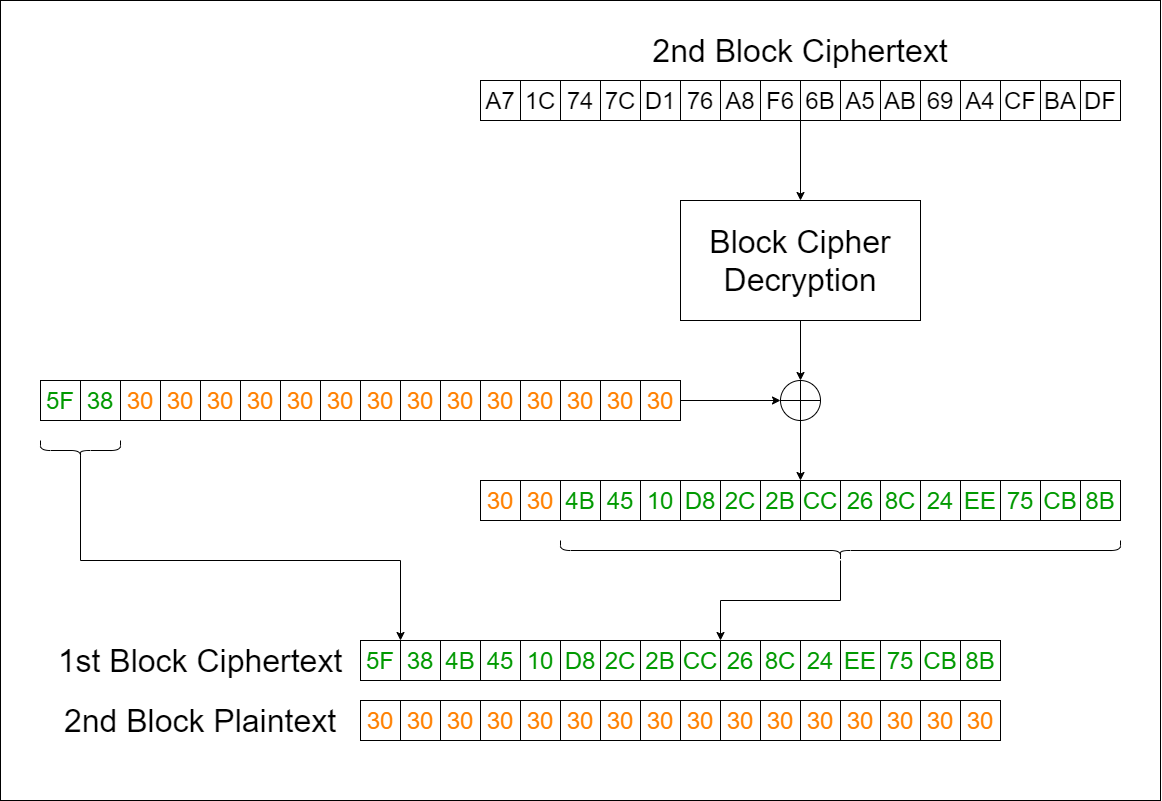
We’ll decrypt the second block using the first block as the IV. The last 14 bytes of the decrypted result are the 14 bytes missing from the first block. To recover the original IV, we can decrypt the first block (now fully recovered) using null bytes as the IV, then XOR with the first block of plaintext. That way, we get the original IV.
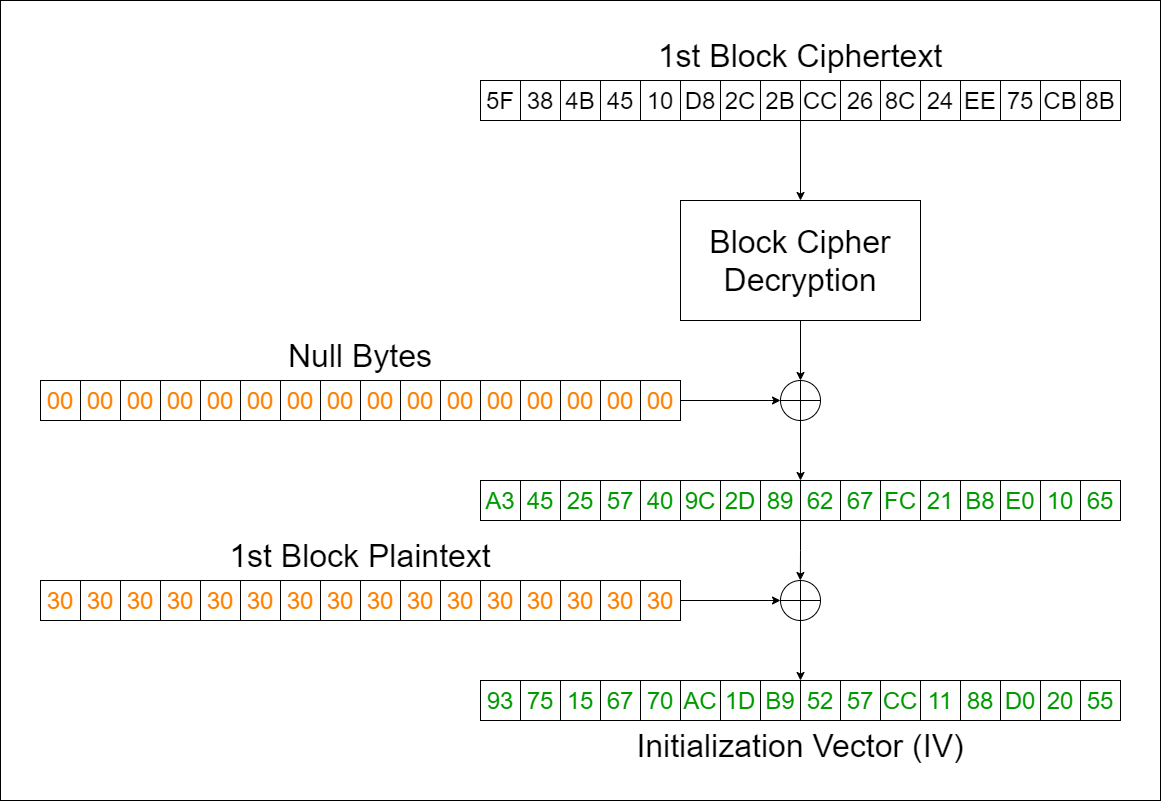
Implementation
#!/usr/bin/python
from Crypto.Cipher import AES
from pwn import xor
import string
'''
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
+ hi all, welcome to the simple KEYBASE cryptography task, try to +
+ decrypt the encrypted message and get the flag as a nice prize! +
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
| Options:
| [G]et the encrypted flag
| [T]est the encryption
| [Q]uit
g
| encrypt(flag) = 438e77d6479cfa357e3fc58fde48028f2dd0bbc5dc2f126db0cb1daf6cd9dd91
| Options:
| [G]et the encrypted flag
| [T]est the encryption
| [Q]uit
t
| Please send your 32 bytes message to encrypt:
00000000000000000000000000000000
| enc = 5f38****************************a71c747cd176a8f66ba5ab69a4cfbadf
| key = 267a269a56464842b12133ae5ca4****
| Options:
| [G]et the encrypted flag
| [T]est the encryption
| [Q]uit
'''
ENCRYPTED_FLAG = '438e77d6479cfa357e3fc58fde48028f2dd0bbc5dc2f126db0cb1daf6cd9dd91'.decode('hex')
ENCRYPTED_ZERO = ['5f38'.decode('hex'), 'a71c747cd176a8f66ba5ab69a4cfbadf'.decode('hex')]
KNOWN_14_KEY = '267a269a56464842b12133ae5ca4'.decode('hex')
tmp_iv = ENCRYPTED_ZERO[0] + '0'*14
enc = ENCRYPTED_ZERO[1]
keys = []
for i in range(256):
for j in range(256):
tmp_key = KNOWN_14_KEY + chr(i) + chr(j)
aes = AES.new(tmp_key, AES.MODE_CBC, tmp_iv)
dec = aes.decrypt(enc)
if dec[:2] == '0'*2:
keys.append(tmp_key)
for key in keys:
aes = AES.new(key, AES.MODE_CBC, ENCRYPTED_FLAG[:16])
res = aes.decrypt(ENCRYPTED_FLAG[16:])
if all(x in string.printable for x in res):
print('key: {}'.format(key.encode('hex')))
break
tmp_iv = ENCRYPTED_ZERO[0] + '0'*14
aes = AES.new(key, AES.MODE_CBC, tmp_iv)
dec = aes.decrypt(ENCRYPTED_ZERO[1])
ENCRYPTED_ZERO[0] = ENCRYPTED_ZERO[0] + dec[2:]
aes = AES.new(key, AES.MODE_CBC, '\x00'*16)
dec = aes.decrypt(ENCRYPTED_ZERO[0])
iv = xor(dec, '0')
print('IV: {}'.format(iv.encode('hex')))
aes = AES.new(key, AES.MODE_CBC, iv)
flag = aes.decrypt(ENCRYPTED_FLAG)
print('flag: {}'.format(flag))
$ python solve.py
key: 267a269a56464842b12133ae5ca44d52
IV: 9375156770ac1db95257cc1188d02055
flag: CCTF{h0W_R3cOVER_7He_5eCrET_1V?}
Symbols
We only get an image file with some math symbols made using LaTeX.
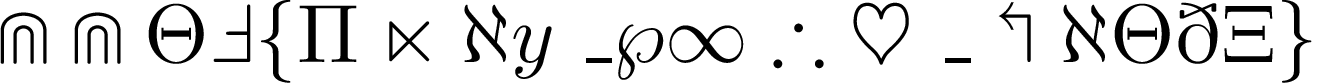
Solution
We find out the which LaTeX syntax is used in the challenge, and the flag is the first letter of each syntax.
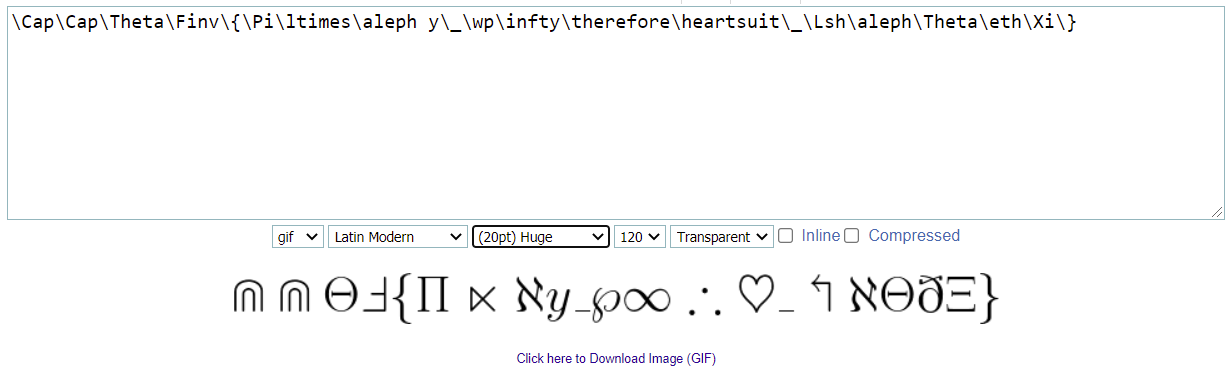
CCTF{Play_with_LaTeX}
Hamul
We get hamul.py and output.txt files.
#!/usr/bin/env python3
from Crypto.Util.number import *
from flag import flag
nbit = 64
while True:
p, q = getPrime(nbit), getPrime(nbit)
P = int(str(p) + str(q))
Q = int(str(q) + str(p))
PP = int(str(P) + str(Q))
QQ = int(str(Q) + str(P))
if isPrime(PP) and isPrime(QQ):
break
n = PP * QQ
m = bytes_to_long(flag.encode('utf-8'))
if m < n:
c = pow(m, 65537, n)
print('n =', n)
print('c =', c)
n = 98027132963374134222724984677805364225505454302688777506193468362969111927940238887522916586024601699661401871147674624868439577416387122924526713690754043
c = 42066148309824022259115963832631631482979698275547113127526245628391950322648581438233116362337008919903556068981108710136599590349195987128718867420453399
Solution
The challenge lies in how the RSA primes are generated. The prime formation is illustrated as follows:
Let A,B,C,D,E,F,G,H,I,J,K,L represent digits
p = ABCDEF -> P = ABCDEFGHIJKL -> PP = ABCDEFGHIJKLGHIJKLABCDEF
q = GHIJKL -> Q = GHIJKLABCDEF -> QQ = GHIJKLABCDEFABCDEFGHIJKL
The solution approach is similar to Midnight Sun CTF 2019 Qual: open-gyckel-crypto and S4CTF 2021: Baby RSA. However, in this challenge, we don’t really know the exact number of base-10 digits in variables $ p $ and $ q $ (between 19-20).
The solution I used was to guess the number of digits in variables $ p $ and $ q $. Since the bruteforce space is very small, this can be a quick solution despite having many unknown variables in its implementation.
Implementation
#!/usr/bin/env python3
from gmpy2 import *
c = 42066148309824022259115963832631631482979698275547113127526245628391950322648581438233116362337008919903556068981108710136599590349195987128718867420453399
e = 65537
n = 98027132963374134222724984677805364225505454302688777506193468362969111927940238887522916586024601699661401871147674624868439577416387122924526713690754043
pq = n
def find():
for i in range(16):
for a1 in range(38, 43):
for a2 in range(38, 43):
for a3 in range(38, 43):
for a4 in range(38, 43):
for a5 in range(70, 90):
ab = (int(str(pq)[:a1]) - i) * 10**a2 + int(str(pq)[-a3:])
a2_p_b2 = (pq - ab * 10**a5 - ab) // 10**a4
try:
a_p_b, ok = iroot(a2_p_b2 + 2 * ab, 2)
if ok:
return int(a_p_b)
except:
continue
a_p_b = find()
for i in range(256):
p_p_q = a_p_b * 10 ** i + a_p_b
phi = n+1 - p_p_q
d = invert(e, phi)
m = pow(c, d, n)
flag = int.to_bytes(int(m), 72, 'big')
if b'CCTF' in flag:
print(flag.strip(b'\x00').decode())
$ python3 solve.py
CCTF{wH3Re_0Ur_Br41N_Iz_5uP3R_4CtIVe_bY_RSA!!}
Rima
We get 3 files: rima.py, g.enc, and h.enc.
#!/usr/bin/env python
from Crypto.Util.number import *
from flag import FLAG
def nextPrime(n):
while True:
n += (n % 2) + 1
if isPrime(n):
return n
f = [int(x) for x in bin(int(FLAG.hex(), 16))[2:]]
f.insert(0, 0)
for i in range(len(f)-1): f[i] += f[i+1]
a = nextPrime(len(f))
b = nextPrime(a)
g, h = [[_ for i in range(x) for _ in f] for x in [a, b]]
c = nextPrime(len(f) >> 2)
for _ in [g, h]:
for __ in range(c): _.insert(0, 0)
for i in range(len(_) - c): _[i] += _[i+c]
g, h = [int(''.join([str(_) for _ in __]), 5) for __ in [g, h]]
for _ in [g, h]:
if _ == g:
fname = 'g'
else:
fname = 'h'
of = open(f'{fname}.enc', 'wb')
of.write(long_to_bytes(_))
of.close()
Solution
To solve this challenge, I reversed the code from bottom to top to recover the flag. First, we need to find out the length of variable $ f $. I compared the lengths of g.enc and h.enc outputs to find the value of $ f $.
from deom import *
gg = open('g.enc', 'rb').read()
hh = open('h.enc', 'rb').read()
gg = digits(int.from_bytes(gg, 'big'), 5)
hh = digits(int.from_bytes(hh, 'big'), 5)
print(len(gg))
print(len(hh))
for f in range(0, 512, 8):
a = next_prime(f)
b = next_prime(a)
g = f * a
h = f * b
c = next_prime(f >> 2)
if g + c == len(gg) and h + c == len(hh):
print(f, g+c, h+c)
break
$ python3 solve.py
65859
67395
256 65859 67395
The correct value for $ f $ is 256, so the flag length is $ \frac{256}{8} = 32 $ characters.
Implementation
#!/usr/bin/env python3
from deom import *
gg = open('g.enc', 'rb').read()
hh = open('h.enc', 'rb').read()
gg = digits(int.from_bytes(gg, 'big'), 5)
hh = digits(int.from_bytes(hh, 'big'), 5)
print(len(gg))
print(len(hh))
# for f in range(0, 512, 8):
# a = next_prime(f)
# b = next_prime(a)
# g = f * a
# h = f * b
# c = next_prime(f >> 2)
# if g + c == len(gg) and h + c == len(hh):
# print(f, g+c, h+c)
# break
f = 256
c = next_prime(f >> 2)
gg = list(map(int, gg))
hh = list(map(int, hh))
for i in range(len(gg)-c-1, -1, -1):
gg[i] = gg[i] - gg[i+c]
for i in range(len(hh)-c-1, -1, -1):
hh[i] = hh[i] - hh[i+c]
gg = gg[c:]
hh = hh[c:]
gg = gg[:f]
hh = hh[:f]
for i in range(f-1-1, -1, -1):
gg[i] = gg[i] - gg[i+1]
res = ''.join(str(x) for x in gg)
flag = int.to_bytes(int(res, 2), 32, 'big').decode()
print(flag)
$ python3 solve.py
65859
67395
CCTF{_how_finD_7h1s_1z_s3cr3T?!}
Tuti
We only get tuti.py as the attachment file.
#!/usr/bin/env python3
from Crypto.Util.number import *
from flag import flag
l = len(flag)
m_1, m_2 = flag[: l // 2], flag[l // 2:]
x, y = bytes_to_long(m_1), bytes_to_long(m_2)
k = '''
000bfdc32162934ad6a054b4b3db8578674e27a165113f8ed018cbe9112
4fbd63144ab6923d107eee2bc0712fcbdb50d96fdf04dd1ba1b69cb1efe
71af7ca08ddc7cc2d3dfb9080ae56861d952e8d5ec0ba0d3dfdf2d12764
'''.replace('\n', '')
assert((x**2 + 1)*(y**2 + 1) - 2*(x - y)*(x*y - 1) == 4*(int(k, 16) + x*y))
Solution
The idea is that we need to find values of $ x $ and $ y $ that satisfy the equation above.
- $ (x^{2} + 1) (y^{2} + 1) - 2(x - y) (xy - 1) = 4(k + xy) $
- $ x^{2} y^{2} + x^{2} + y^{2} + 1 - 2(x^{2}y - x - xy^{2} + y) = 4(k + xy) $
- $ x^{2} y^{2} + x^{2} + y^{2} + 1 - 2x^{2}y + 2x + 2xy^{2} - 2y = 4k + 4xy $
At this point, assume $ u = y^{2} $ to simplify the equation.
- $ ux^{2} + x^{2} + u + 1 - 2x^{2}y + 2x + 2ux - 2y = 4k + 4xy $
- $ ux^{2} + 2ux + u + x^{2} + 2x + 1 - 2x^{2}y - 2y = 4k + 4xy $
- $ (ux + u)(x + 1) + (x + 1)(x + 1) - 2x^{2}y - 2y = 4k + 4xy $
- $ (ux + u)(x + 1) + (x + 1)(x + 1) - 2x^{2}y - 2y - 4xy = 4k $
- $ u(x + 1)(x + 1) + (x + 1)(x + 1) - 2x^{2}y - 2y - 4xy = 4k $
Substitute $ y^{2} $ back into $ u $.
- $ y^{2}(x + 1)(x + 1) + (x + 1)(x + 1) - 2x^{2}y - 2y - 4xy = 4k $
- $ y^{2}(x + 1)^{2} + (x + 1)^{2} - 2x^{2}y - 2y - 4xy = 4k $
- $ (y^{2} + 1)(x + 1)^{2} - 2x^{2}y - 2y - 4xy = 4k $
- $ (y^{2} + 1)(x + 1)^{2} - 2y (x^{2} + 2x + 1) = 4k $
- $ (y^{2} + 1)(x + 1)^{2} - 2y (x + 1)^{2} = 4k $
- $ (y^{2} - 2y + 1)(x + 1)^{2} = 4k $
- $ (y - 1)^{2}(x + 1)^{2} = 4k $
- $ \sqrt{(y - 1)^{2}(x + 1)^{2}} = \sqrt{2^{2}k} $
- $ (y - 1)(x + 1) = 2 \sqrt{k} $
We can see that $ 2 \sqrt{k} $ is the product of $ y-1 $ and $ x+1 $. Using the divisors function from the sage.arith.misc module, we can find values of $ y-1 $ and $ x+1 $ that satisfy the equation.
Implementation
from Crypto.Util.number import *
from gmpy2 import *
from sage.all import *
k = '''
000bfdc32162934ad6a054b4b3db8578674e27a165113f8ed018cbe9112
4fbd63144ab6923d107eee2bc0712fcbdb50d96fdf04dd1ba1b69cb1efe
71af7ca08ddc7cc2d3dfb9080ae56861d952e8d5ec0ba0d3dfdf2d12764
'''.replace('\n', '')
k = iroot(int(k, 16), 2)
assert k[1]
k = int(k[0]) * 2
print(k)
ks = divisors(k)
print(len(ks))
# (y-1)*(x+1) == 2*sqrt(k)
isPrintable = lambda x: all(i >= 0x20 and i < 0x7f for i in x)
for tmp in ks:
a = tmp - 1
if not a: continue
b = k // tmp + 1
x = long_to_bytes(a)
y = long_to_bytes(b)
if isPrintable(x) and isPrintable(y):
flag = x+y
if flag.startswith(b'CCTF{'):
print(flag.decode())
$ sage -python solve.py
992752253935874779143952218845275961347009322164731344882417010624071055636710540798045985678351986133612
9216
CCTF{S1mPL3_4Nd_N!cE_Diophantine_EqUa7I0nS!}
Ferman
We are given access to a service at 07.cr.yp.toc.tf 22010 without any attachment files for this challenge. The service provides 3 options:
- Print encrypted flag
- Reveal the parameters
- Quit
$ nc 07.cr.yp.toc.tf 22010
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
+ hi talented participants, welcome to the FERMAN cryptography task! +
+ Solve the given equations and decrypt the encrypted flag! Enjoy! +
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
| Parameters generation is a bit time consuming, so please be patient :P
| Options:
| [P]rint encrypted flag
| [R]eveal the parameters
| [Q]uit
p
| encrypt(flag) = 231943209108551364462499001833007833339471858509636903278777063625331785566177786876600883615579527538615449262965247345037039607956522411513272817618458127569994469550455219738226018767357372553130829156939915512881378019724932997157155395756993371652694606158039648511432571482664432642345638869625234178788155010122530376971444998919814539291576949527410495332000913070325460431669781091685926807159246810108562287609768925930433885165034652885839565911250630355513691399221705
| Options:
| [P]rint encrypted flag
| [R]eveal the parameters
| [Q]uit
r
e = 65537
isPrime(p) = True
isPrime(q) = True
n = p * q
(p - 101)**2 + (q - 640)**2 = 12585581867200760491901063218977008095777706525365307913267337889812133401733866376423522953619723513985288148041129036865848253118431620861635892195147618664084314783941500430569307840513730914732163671370801485277342439063100992039682753530924508927481297232132764512175962671321299489617673153858637922542612084091616376653006320421825225775179652753229398478629738230473614938248244076160394614556972508910519652684982889251539480613394248296145136678927126153770492875305723149
m = bytes_to_long(flag)
c = pow(m, e, n)
| Options:
| [P]rint encrypted flag
| [R]eveal the parameters
| [Q]uit
Solution
Disclaimer! This challenge was solved after the competition ended.
During the competition, I tried several methods to get the values of $p$ and $q$ from the equation $(p - a)^{2} (q - b)^{2} = k$, but none worked.
After the competition ended, I tried adding assume(p, "integer") and assume(q, "integer") so that the solution could be found by sage.symbolic.relation.solve. There were several candidate solutions, so they needed to be compared using the Brahmagupta-Fibonacci identity to get the $p$ and $q$ values used by the service.
Implementation
from sage.all import *
from Crypto.Util.number import *
import gmpy2
k7 = 12585581867200760491901063218977008095777706525365307913267337889812133401733866376423522953619723513985288148041129036865848253118431620861635892195147618664084314783941500430569307840513730914732163671370801485277342439063100992039682753530924508927481297232132764512175962671321299489617673153858637922542612084091616376653006320421825225775179652753229398478629738230473614938248244076160394614556972508910519652684982889251539480613394248296145136678927126153770492875305723149
k = gmpy2.iroot(k7, 7)
assert k[1]
k = Integer(k[0])
print(f'{k = }')
p = var('p')
q = var('q')
assume(p, "integer")
assume(q, "integer")
res = solve(p ** 2 + q ** 2 == k, p, q)
res = [(Integer(p), Integer(q)) for p, q in res if p > 0 and q > 0]
a = 101
b = 640
c = 231943209108551364462499001833007833339471858509636903278777063625331785566177786876600883615579527538615449262965247345037039607956522411513272817618458127569994469550455219738226018767357372553130829156939915512881378019724932997157155395756993371652694606158039648511432571482664432642345638869625234178788155010122530376971444998919814539291576949527410495332000913070325460431669781091685926807159246810108562287609768925930433885165034652885839565911250630355513691399221705
e = 65537
def mul(r, s):
a, b = r
c, d = s
x1 = a * c - b * d
y1 = a * d + b * c
x2 = a * c + b * d
y2 = a * d - b * c
return (abs(x1), abs(y1)), (abs(x2), abs(y2))
def sqr(r):
return mul(r, r)[0]
def find(res):
for r in res:
r2 = sqr(r)
r4 = sqr(r2)
for r3 in mul(r, r2):
for r7 in mul(r4, r3):
p, q = r7
assert p ** 2 + q ** 2 == k ** 7
p += a
q += b
if is_prime(p) and is_prime(q):
return [p, q]
p, q = find(res)
n = p * q
d = gmpy2.invert(e, (p-1)*(q-1))
flag = long_to_bytes(pow(c, d, n)).decode()
print(flag)
$ sage -python solve.sage
k = 535245874316620332296772953273538077513756072907285297884311803942949
CCTF{Congrats_Y0u_5OLv3d_x**2+y**2=z**7}
Salt and Pepper
We’re given the attachment salt_pepper.py and a service at 02.cr.yp.toc.tf 28010.
#!/usr/bin/env python3
from hashlib import md5, sha1
import sys
from secret import salt, pepper
from flag import flag
assert len(salt) == len(pepper) == 19
assert md5(salt).hexdigest() == '5f72c4360a2287bc269e0ccba6fc24ba'
assert sha1(pepper).hexdigest() == '3e0d000a4b0bd712999d730bc331f400221008e0'
def auth_check(salt, pepper, username, password, h):
return sha1(pepper + password + md5(salt + username).hexdigest().encode('utf-8')).hexdigest() == h
def die(*args):
pr(*args)
quit()
def pr(*args):
s = " ".join(map(str, args))
sys.stdout.write(s + "\n")
sys.stdout.flush()
def sc():
return sys.stdin.readline().strip()
def main():
border = "+"
pr(border*72)
pr(border, " welcome to hash killers battle, your mission is to login into the ", border)
pr(border, " ultra secure authentication server with provided information!! ", border)
pr(border*72)
USERNAME = b'n3T4Dm1n'
PASSWORD = b'P4s5W0rd'
while True:
pr("| Options: \n|\t[L]ogin to server \n|\t[Q]uit")
ans = sc().lower()
if ans == 'l':
pr('| send your username, password as hex string separated with comma: ')
inp = sc()
try:
inp_username, inp_password = [bytes.fromhex(s) for s in inp.split(',')]
except:
die('| your input is not valid, bye!!')
pr('| send your authentication hash: ')
inp_hash = sc()
if USERNAME in inp_username and PASSWORD in inp_password:
if auth_check(salt, pepper, inp_username, inp_password, inp_hash):
die(f'| Congrats, you are master in hash killing, and it is the flag: {flag}')
else:
die('| your credential is not valid, Bye!!!')
else:
die('| Kidding me?! Bye!!!')
elif ans == 'q':
die("Quitting ...")
else:
die("Bye ...")
if __name__ == '__main__':
main()
Solution
Disclaimer! This challenge is solved after competition.
The main challenge lies in the auth_check function:
def auth_check(salt, pepper, username, password, h):
return sha1(pepper + password + md5(salt + username).hexdigest().encode('utf-8')).hexdigest() == h
The salt and pepper variables are unknown, but we know their md5sum, sha1sum, and lengths. This indicates a typical hash length extension attack, where we can add some bits of a certain length to guess the checksum, even though we don’t know the contents of these variables. There are several tools that can help us perform hash length extension attacks, one of them being hashpump. However, for some reason, the hashpump I used produced different output, so it needed to be ‘tweaked’ to find valid results.
Implementation
#!/usr/bin/env python3
from pwn import *
import hashpumpy, re
MD5_v0 = '5f72c4360a2287bc269e0ccba6fc24ba'
MD5_v1 = 'a'
MD5_v2 = 'n3T4Dm1n'
MD5_v3 = 19-1
SHA_v0 = '3e0d000a4b0bd712999d730bc331f400221008e0'
SHA_v1 = 'a'
SHA_v2 = 'P4s5W0rd'
SHA_v3 = 19-1
r = remote('02.cr.yp.toc.tf', 28010, level='warn')
# r = process(['python3', 'dup.py'], level='warn')
r.sendline('l')
z_md5 = hashpumpy.hashpump(MD5_v0, MD5_v1, MD5_v2, MD5_v3)
z_md5_hash, z_md5_payload = z_md5
print(z_md5_hash)
z_sha = hashpumpy.hashpump(SHA_v0, SHA_v1, SHA_v2 + z_md5_hash, SHA_v3)
z_sha_hash, z_sha_payload = z_sha
print(z_sha_hash)
username = z_md5_payload[1:]
password = z_sha_payload[1:-32]
print(repr(username))
print(repr(password))
r.sendline(f'{username.hex()},{password.hex()}')
r.recvuntil('authentication hash:')
r.sendline(z_sha_hash)
r.recvline(0)
res = r.recvline(0).decode()
res = re.findall(r'CCTF{(.+)}', res)[0]
print('CCTF{\%s}' % (res))
$ python3 solve.py
...
95623660d3d04c7680a52679e35f041c
...
83875efbe020ced3e2c5ecc908edc98481eba47f
b'\x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x98\x00\x00\x00\x00\x00\x00\x00n3T4Dm1n'
b'\x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x98P4s5W0rd'
...
CCTF{Hunters_Killed_82%_More_Wolves_Than_Quota_Allowed_in_Wisconsin}
Wolf
We are given the Wolf.py attachment file and access to a service at 01.cr.yp.toc.tf 27010.
#!/usr/bin/env python3
from Cryptodome.Cipher import AES
import os, time, sys, random
from flag import flag
passphrase = b'HungryTimberWolf'
def encrypt(msg, passphrase, niv):
msg_header = 'EPOCH:' + str(int(time.time()))
msg = msg_header + "\n" + msg + '=' * (15 - len(msg) % 16)
aes = AES.new(passphrase, AES.MODE_GCM, nonce = niv)
enc = aes.encrypt_and_digest(msg.encode('utf-8'))[0]
return enc
def die(*args):
pr(*args)
quit()
def pr(*args):
s = " ".join(map(str, args))
sys.stdout.write(s + "\n")
sys.stdout.flush()
def sc():
return sys.stdin.readline().strip()
def main():
border = "+"
pr(border*72)
pr(border, " hi wolf hunters, welcome to the most dangerous hunting ground!! ", border)
pr(border, " decrypt the encrypted message and get the flag as a nice prize! ", border)
pr(border*72)
niv = os.urandom(random.randint(1, 11))
flag_enc = encrypt(flag, passphrase, niv)
while True:
pr("| Options: \n|\t[G]et the encrypted flag \n|\t[T]est the encryption \n|\t[Q]uit")
ans = sc().lower()
if ans == 'g':
pr(f'| encrypt(flag) = {flag_enc.hex()}')
elif ans == 't':
pr("| Please send your message to encrypt: ")
msg_inp = sc()
enc = encrypt(msg_inp, passphrase, niv).hex()
pr(f'| enc = {enc}')
elif ans == 'q':
die("Quitting ...")
else:
die("Bye ...")
if __name__ == '__main__':
main()
Solution
There is a bug in the following code:
niv = os.urandom(random.randint(1, 11))
flag_enc = encrypt(flag, passphrase, niv)
When we connect to the service multiple times, we have a probability of $\frac{1}{11}$ or about 9% chance of getting randint(1, 11) to return 1. The idea is to collect several encrypted flags by repeatedly connecting to the service, hoping to receive an encrypted flag with a 1-byte nonce. This way, we only need to brute force 1 byte of nonce since the AES-GCM passphrase is known from the provided source code.
Implementation
#!/usr/bin/env python3
from pwn import *
from Crypto.Cipher import AES
while True:
r = remote('01.cr.yp.toc.tf', 27010, level='warn')
r.sendline('g')
r.recvuntil('encrypt(flag) = ')
ct = r.recvline(0).decode()
r.close()
for ni in range(256):
niv = bytes([ni])
aes = AES.new(b'HungryTimberWolf', AES.MODE_GCM, nonce = niv)
flag = aes.decrypt(bytes.fromhex(ct))
if b'EPOCH' in flag:
print(flag.decode())
exit()
$ python3 solve.py
...
EPOCH:1628059598
CCTF{____w0lveS____c4n____be____dan9er0uS____t0____p3oplE____!!!!!!}===========
