ångstromCTF is a CTF event organized by Montgomery Blair High School. This CTF had 5 challenge categories, including cryptography. I managed to solve 11 out of 12 challenges, but I’ll only write up 2 of them here:
- Substitution (130 points, 140 solves)
- Oracle of Blair (160 points, 139 solves)
Substitution
nc crypto.2021.chall.actf.co 21601
Author: EvilMuffinHa
Challenge
We’re given a source code and access to a service at crypto.2021.chall.actf.co 21601.
#!/usr/bin/python
from functools import reduce
with open("flag", "r") as f:
key = [ord(x) for x in f.read().strip()]
def substitute(value):
return (reduce(lambda x, y: x*value+y, key))%691
print("Enter a number and it will be returned with our super secret synthetic substitution technique")
while True:
try:
value = input("> ")
if value == 'quit':
quit()
value = int(value)
enc = substitute(value)
print(">> ", end="")
print(enc)
except ValueError:
print("Invalid input. ")
Solution
Our integer input gets used as an argument in the substitute function. The substitute function processes the value using key, where the key values are taken from the flag characters. If we break it down, the substitute function has this equation:
key[0]*x^(n) + key[1]*x^(n-1) + key[2]*x^(n-2) + ... + key[n] mod 691
where $ x $ is the value parameter. To recover all coefficients, we can use Lagrange Polynomial. To use Lagrange, we need to get at least $ n $ pairs of $ x $ and $ y $ (in this case, enc) first, where $ n $ is the flag length. Since we don’t know the flag length, we’ll assume it’s less than 256 characters, so we only need to get 256 pairs of $ x $ and $ y $.
Implementation
from pwn import *
r = remote('crypto.2021.chall.actf.co', 21601)
cts = []
for i in range(256):
r.sendlineafter('> ', str(i))
cts.append(int(r.recvline(0).split(' ')[1]))
print cts
[125, 492, 670, 39, 244, 257, 104, 615, 129, 520, 428, 599, 404, 468, 465, 523, 345, 44, 425, 515, 116, 120, 515, 283, 651, 199, 69, 388, 319, 410, 133, 267, 215, 352, 521, 270, 629, 564, 662, 640, 352, 351, 481, 103, 161, 106, 306, 360, 587, 318, 450, 314, 164, 185, 519, 85, 472, 343, 41, 652, 320, 581, 400, 259, 119, 525, 374, 434, 162, 661, 145, 360, 209, 302, 426, 285, 358, 610, 572, 366, 434, 627, 206, 427, 166, 527, 590, 189, 462, 148, 428, 140, 306, 163, 265, 249, 522, 66, 136, 332, 327, 51, 337, 173, 100, 23, 445, 523, 252, 655, 105, 391, 322, 127, 196, 476, 116, 58, 404, 218, 492, 60, 194, 479, 175, 390, 12, 66, 270, 227, 41, 189, 428, 3, 68, 356, 228, 101, 285, 93, 620, 94, 490, 411, 422, 161, 152, 258, 26, 588, 406, 382, 32, 140, 484, 114, 180, 483, 38, 397, 155, 206, 141, 599, 584, 589, 460, 68, 520, 617, 247, 243, 331, 339, 239, 323, 533, 159, 28, 491, 663, 115, 441, 451, 617, 267, 188, 222, 472, 483, 500, 576, 117, 517, 228, 545, 329, 14, 18, 411, 478, 247, 349, 322, 298, 287, 601, 520, 59, 177, 98, 150, 286, 587, 402, 494, 318, 269, 189, 527, 207, 154, 291, 538, 192, 161, 317, 485, 466, 119, 117, 123, 20, 120, 276, 24, 435, 672, 573, 676, 58, 596, 648, 126, 428, 183, 524, 133, 232, 281, 190, 169, 655, 314, 29, 378]
PRIME = 691
F = FiniteField(PRIME)
P = F['x']
points = [125, 492, 670, 39, 244, 257, 104, 615, 129, 520, 428, 599, 404, 468, 465, 523, 345, 44, 425, 515, 116, 120, 515, 283, 651, 199, 69, 388, 319, 410, 133, 267, 215, 352, 521, 270, 629, 564, 662, 640, 352, 351, 481, 103, 161, 106, 306, 360, 587, 318, 450, 314, 164, 185, 519, 85, 472, 343, 41, 652, 320, 581, 400, 259, 119, 525, 374, 434, 162, 661, 145, 360, 209, 302, 426, 285, 358, 610, 572, 366, 434, 627, 206, 427, 166, 527, 590, 189, 462, 148, 428, 140, 306, 163, 265, 249, 522, 66, 136, 332, 327, 51, 337, 173, 100, 23, 445, 523, 252, 655, 105, 391, 322, 127, 196, 476, 116, 58, 404, 218, 492, 60, 194, 479, 175, 390, 12, 66, 270, 227, 41, 189, 428, 3, 68, 356, 228, 101, 285, 93, 620, 94, 490, 411, 422, 161, 152, 258, 26, 588, 406, 382, 32, 140, 484, 114, 180, 483, 38, 397, 155, 206, 141, 599, 584, 589, 460, 68, 520, 617, 247, 243, 331, 339, 239, 323, 533, 159, 28, 491, 663, 115, 441, 451, 617, 267, 188, 222, 472, 483, 500, 576, 117, 517, 228, 545, 329, 14, 18, 411, 478, 247, 349, 322, 298, 287, 601, 520, 59, 177, 98, 150, 286, 587, 402, 494, 318, 269, 189, 527, 207, 154, 291, 538, 192, 161, 317, 485, 466, 119, 117, 123, 20, 120, 276, 24, 435, 672, 573, 676, 58, 596, 648, 126, 428, 183, 524, 133, 232, 281, 190, 169, 655, 314, 29, 378]
shares = [(F(i), F(c)) for i, c in enumerate(points)]
coefs = P.lagrange_polynomial(shares)
coefs = [chr(x) for x in coefs]
print ''.join(coefs)[::-1]
Flag
actf{polynomials_20a829322766642530cf69}
Oracle of Blair
Not to be confused with the ORACLE of Blair
nc crypto.2021.chall.actf.co 21112
Author: lamchcl
Challenge
We’re given a source code and access to a service at crypto.2021.chall.actf.co 21112.
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
import os
key = os.urandom(32)
flag = open("flag","rb").read()
while 1:
try:
i = bytes.fromhex(input("give input: "))
if not i:
break
except:
break
iv = os.urandom(16)
inp = i.replace(b"{}", flag)
if len(inp) % 16:
inp = pad(inp, 16)
print(
AES.new(key, AES.MODE_CBC, iv=iv).decrypt(inp).hex()
)
Solution
The input must be in hex format, and when decoded, it should contain the string {} which the program will replace with the flag. The key and IV are 32 and 16 random bytes respectively. The IV gets regenerated each time the program decrypts an input.
In this case, we can put the {} string anywhere we want, so we can work around the random IV to get specific plaintext blocks.
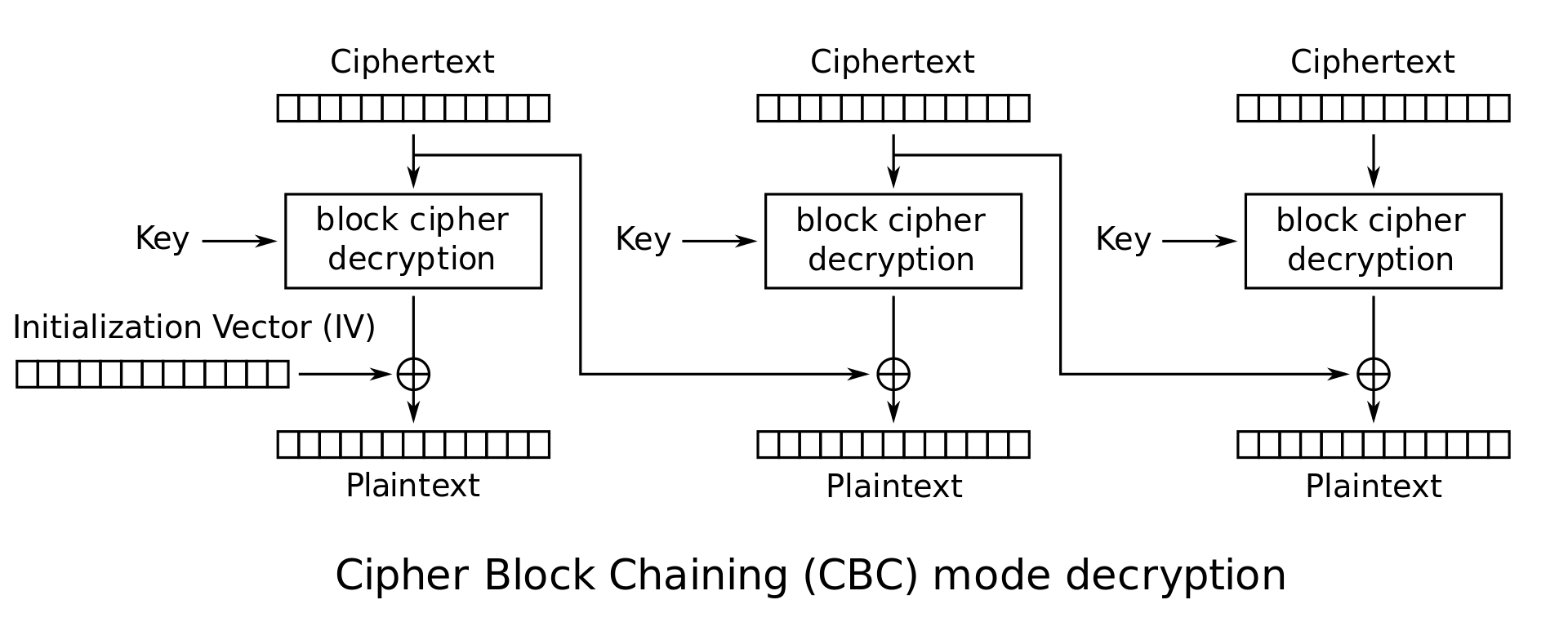
The idea is to input a payload that has an extra block after the flag block. This way, the plaintext of the extra block will be the result of XORing the intermediate block with the previous block (the flag block). How do we know the intermediate block of the extra block? We can work around it by making the extra block the same as the block before the flag. To make sure the block before the flag isn’t affected by random IV bytes, we need to add a dummy block before it.
But remember, the idea above can only be implemented when we know the flag length. To find the exact flag length, we can try inputting different numbers of characters and observe when the number of plaintext blocks increases.
def panjang_flag():
for i in range(16):
pload = '{}' + 'A'*i
print i, pload, len(kirim(pload))
panjang_flag()
0 {} 32
1 {}A 32
2 {}AA 32
3 {}AAA 32
4 {}AAAA 32
5 {}AAAAA 32
6 {}AAAAAA 32
7 {}AAAAAAA 32
8 {}AAAAAAAA 48
9 {}AAAAAAAAA 48
10 {}AAAAAAAAAA 48
11 {}AAAAAAAAAAA 48
12 {}AAAAAAAAAAAA 48
13 {}AAAAAAAAAAAAA 48
14 {}AAAAAAAAAAAAAA 48
15 {}AAAAAAAAAAAAAAA 48
In this case, the flag length is 32 - 7 = 25 chars, so we need to recover two flag blocks. The method is similar, but for the first flag block, we’ll use the second flag block as the extra block. Here’s the code:
Implementation
from deom import *
r = remote('crypto.2021.chall.actf.co', 21112)
def kirim(pload):
r.sendlineafter('give input: ', pload.encode('hex'))
return r.recvline(0).decode('hex')
LEN = 25
print 'LEN', LEN
# ==================================================
pt = 'A'*32 + '{}' + 'A'*(16 - (LEN % 16)) + 'A'*16 # 5 blocks
ct = kirim(pt)
cts = [ct[i:i+16] for i in range(0, len(ct), 16)]
print len(cts)
# 2nd flag
inter_a = xor(cts[1], 'A'*16)
flag2 = xor(inter_a, cts[4])
print flag2 # ke_ecb_c}AAAAAAA
pt = flag2 + flag2 + '{}' + 'A'*(16 - (LEN % 16)) + flag2 # 5 blocks
ct = kirim(pt)
cts = [ct[i:i+16] for i in range(0, len(ct), 16)]
print len(cts)
# 1st flag
inter_flag2 = xor(cts[1], flag2)
flag1 = xor(inter_flag2, cts[3])
print flag1 # actf{cbc_more_li
Flag
actf{cbc_more_like_ecb_c}
